
|
Лекция 14. Равновесие потребителя
Множество допустимых возможностей потребителя. Бюджетная линия
В предыдущей лекции мы описали систему предпочтений потребителя. Рассмотрим теперь множество его возможностей, т.е. множество всех доступных потребителю товарных наборов.
Представим, прежде всего, что потребитель располагает в данный период денежной суммой, например, в 1000 руб. Понятно, что истратить эту сумму в принципе можно весьма различными способами: можно купить на все деньги жевательной резинки, можно - учебников по экономике, а можно купить один учебник (конечно, тот, который вы держите сейчас в руках), одну пачку резинки, а на остальные деньги еще чего-нибудь, что душа пожелает. Иными словами, наш потребитель может купить любой набор товаров, удовлетворяющий лишь одному простому требованию: общие расходы на данный набор не превышают суммы денег, находящейся в распоряжении потребителя - 1000 руб.
Сформулируем это правило в более общем виде. Пусть потребитель располагает в единицу времени некоторым доходом М. Отметим, что экономиста в данном случае совершенно не интересует источник этого дохода (были ли деньги заработаны, взяты в долг или выручены от продажи имущества), важно лишь, что потребитель в течение данного периода не может расходовать свыше М денежных единиц. Тогда, как уже говорилось выше, потребитель может приобрести любой набор товаров Х = (x1, x2, ..., xn), удовлетворяющий следующему условию:
где x1, x2, ..., xn — количество единиц товаров 1, 2,..., n, приобретаемых потребителем; , P2,..., Pn — цены этих товаров; М — располагаемый доход потребителя.
Выражение (1) называется бюджетным ограничением потребителя. Вспомним, что графические методы анализа заставляют нас рассматривать случай, когда потребительский выбор ограничен двумя товарами (назовем их товар Х и Y). Тогда бюджетное ограничение имеет вид
Для того чтобы представить множество товарных наборов, удовлетворяющих ограничению (2) в графическом пространстве товаров, нам необходимо, очевидно, отобразить в пространстве товаров границу этого множества, т.е. линию
Линия, описываемая уравнением (3), носит название бюджетной линии.
Примем теперь очень важное предположение:
предположим, что отдельный потребитель не может повлиять на цену какого-либо товара, сколь значительно бы этот потребитель не изменял свой объем потребления данного товара (иными словами, на рынке существует совершенная конкуренция на стороне спроса). В самом деле, трудно себе представить, чтобы доля отдельного потребителя на рынке некоторых потребительских товаров (продуктов питания, одежды, обуви, бытовой техники и т.д.) была столь велика, чтобы изменение спроса одного лишь потребителя, например, на мясные продукты или магнитофонные кассеты могло бы привести к изменению цены на эти товары. Таким образом, цены товаров выступают для потребителя как некие внешние, заданные рынком величины.
Вернемся теперь к уравнению (3) и попробуем представить бюджетную линию графически. Заметим, что уравнение (3) легко преобразуется в уравнение
Поскольку величины М, РX и РY, по нашему предположению, постоянны, уравнение (4) представляет собой уравнение прямой линии (типа y = ax + b), где М/РY — свободный член, а –РX/РY — коэффициент при переменной х. Бюджетная линия соответственно представляет собой прямую линию типа линии АВ, изображенной на рис. 1.
 Рис. 1.
Рис. 1. Бюджетная линия Координаты точек А и В (точки пересечения бюджетной линии с осями координат) характеризуют максимальные количества товаров Х и Y, которые может приобрести потребитель, истратив весь свой доход только на товар Х или только на товар Y. Так, ордината точки А yA = М/РY. Именно столько товара Y может купить потребитель, вовсе отказавшись от приобретения товара X. Аналогичным образом абсцисса точки В xB = = М/РX. Любой другой находящийся на бюджетной линии набор товаров С = (xc, yc) имеет для потребителя точно такую же стоимость М, что и наборы А = (0, М/РY) и В = (М/РX, 0). Вообще говоря, бюджетная линия - это геометрическое место точек, характеризующих все наборы товаров, которые может приобрести потребитель, полностью израсходовав свой доход М при данных ценах товаров РX и РY.
Как видно из рис. 1, бюджетная линия имеет отрицательный наклон. Такое свойство бюджетной линии вполне объяснимо: поскольку наборы товаров, находящиеся на бюджетной линии, имеют одинаковую стоимость, увеличение объема закупок одного товара возможно лишь за счет сокращения потребления другого товара. Вспомним, что наклон прямой линии характеризуется коэффициентом при переменной х в уравнении этой прямой. Следовательно, наклон бюджетной линии характеризуется величиной РX/РY (см. (4)). Знак “минус” как раз и указывает на отрицательный наклон бюджетной линии (так как цены товаров — положительные величины, т. е. РX > 0, РY > 0, то величина РX/РY отрицательная). Наклон бюджетной линии равен, таким образом, соотношению цен товаров, взятому с противоположным знаком. Наклон этот, как видно, является постоянной величиной, поскольку мы предположили ранее, что отдельный потребитель не способен повлиять на рыночные цены товаров.
Теперь, когда мы уже знаем свойства бюджетной линии, представим графически множество всех наборов товаров, удовлетворяющих бюджетному ограничению.. Поскольку объемы потребления не могут быть отрицательными величинами (x i 0, y i 0), доступное множество представляет собой заштрихованный на рис. 2 треугольник ОАВ, ограниченный бюджетной линией и осями координат.
 Рис. 2.
Рис. 2. Множество возможностей потребителя. K и L - доступные наборы, D и Е - недоступные. Поскольку конечной целью нашего анализа является изучение реакции потребителя на изменение цен и дохода, нам необходимо, очевидно, рассмотреть, как изменяются при изменении цен и доходов границы доступного множества. Начнем с изменения дохода. Пусть первоначально доход потребителя составлял М1. Тогда бюджетная линия описывается уравнением (линия АВ на рис. 3)
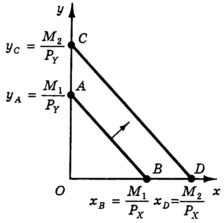 Рис. 3.
Рис. 3. Сдвиг бюджетной линии при изменении дохода Предположим теперь, что доход потребителя увеличился с М1 до а цены товаров остались неизменными. Тогда уравнение новой бюджетной линии имеет вид
Простое сравнение показывает, что коэффициент при переменной х в уравнении (6) остался таким же, как и в уравнении (5), а значит, не изменился наклон бюджетной линии, который определяется соотношением цен. Зато изменились координаты точек пересечения бюджетной линии с осями координат: новая бюджетная линия пересекает ось y в точке С с ординатой yc = М2/PY, а ось x — в точке D с абсциссой xD = = М2/PX. Таким образом, увеличение дохода при неизменных ценах приводит к параллельному сдвигу бюджетной линии вверх (а снижение дохода соответственно к параллельному сдвигу бюджетной линии вниз, доказательство чего предоставим читателю).
Вернемся теперь к первоначальной бюджетной линии АВ, описываемой уравнением (5), и рассмотрим еще одну весьма важную в экономике ситуацию: пусть теперь изменится цена лишь одного товара Х (например, уменьшится с PX до PX1), в то время как цена товара Y и доход потребителя останутся неизменными. Тогда новое бюджетное ограничение примет вид
В этом случае коэффициент при переменной х изменится с –PX/PY на –PX1/PY, а следовательно, изменится и наклон бюджетной линии. Неизменной останется точка пересечения бюджетной линии с осью y — точка А. Поскольку доход М1, и цена PY не изменились, максимально возможный объем закупок потребителем товара Y по-прежнему составляет М1/PY единиц товара Y. В то же время точка пересечения бюджетной линии с осью х сместилась вправо (рис. 4).
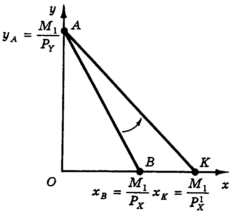 Рис. 4.
Рис. 4. Поворот бюджетной линии при изменении дохода Если первоначальная бюджетная линия пересекает ось х в точке В с абсциссой xB = М1/PY, то “новая” бюджетная линия (при цене PX1 < PX пересекает ось х в точке K с абсциссой xk = М1/PX1. Иными словами, поскольку цена товара Х уменьшилась, потребитель может теперь, израсходовав весь свой доход на товар X, купить большее количество единиц этого товара. Таким образом, уменьшение цены товара Х приводит к повороту бюджетной линии против часовой стрелки вокруг точки пересечения бюджетной линии с осью y (а увеличение цены товара Х — к аналогичному повороту по часовой стрелке).
|